Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

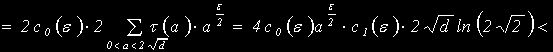
, где

Теорема доказана.

О диагональных формах и оценка снизу числа классов в роде

В этом параграфе мы получим одну оценку снизу для числа классов в роде неопределенных бинарных квадратичных форм. Сначала введем соответствующие понятия.

Определение 1. Целое число , не делящееся на простое число , называется квадратичным вычетом по модулю простого числа, если число  сравнимо с квадратом некоторого целого числа по модулю , т.е.  — квадратичный вычет по модулю , если сравнение  имеет решение; в противном случае число  называется квадратичным невычетом по модулю . В теории квадратичных вычетов очень полезно использование так называемого символа Лежандра.

Определение 2. Символом Лежандра  числа  по простому модулю , которое определяется следующим соотношением:

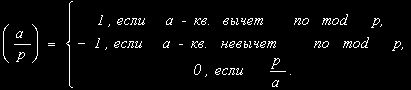
Приведем некоторые основные свойства символа Лежандра, которые нам понадобятся.

Свойство 1 . 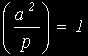, если

Свойство 2 . Если , то  (свойство периодичности)

Свойство 3 . 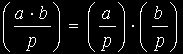 (свойство мультипликативности)

Свойство 4 . , если

Определим теперь понятие рода квадратичных форм, впервые введенное Гауссом. Совокупность классов собственно примитивного порядка данного дискриминанта  Гаусс в своей арифметической теории квадратичных форм разделяет на ряды, относя в один и тот же род все те классы, формы которых имеют и тот же «характер». Под характером примитивной формы или примитивного класса форм Гаусс понимает следующее.

Пусть — простой делитель дискриминанта , и пусть число всех этих различных модулей  равно . Можно показать, что если  — один из этих  модулей, то для всех чисел , представимых данной собственно примитивной формой дискриминанта  и взаимно простых с , символы Лежандра  имеют одно и то же значение. В самом деле, пусть

 — собственно примитивная форма дискриминанта  и  — любой нечетный простой делитель числа , и ,  — два числа, представляемых формой  и не делящихся на . Подстановка 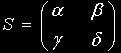 определителя  переводит  в форму  (см. соотношения (3) §1), причем , откуда , т.е. в силу определения символа Лежандра имеем . Из этого равенства в очередь на основании свойств 3 и 4следует, что .

Символ Лежандра  имеет одно и то же значение для всех чисел , представляемых формой . Выпишем эти символы Лежандра, которые все равны  или  для всех  указанных модулей , взятых в определенном выбранном порядке.

Тогда для данной квадратичной формы получается некоторая определенная последовательность  чисел, равных . Эта последовательность чисел, равных  , и называется характером рассматриваемой собственно примитивной бинарной квадратичной формы дискриминанта  или характером класса этой формы.

Так как число всех различных последовательностей, составленных из  членов, равных  или  равно , то число различных характеров форм данного дискриминанта, а следовательно, и число родов не больше, чем . Чтобы решить вопрос о точном числе родов, Гаусс вводит в рассмотрение операции композиции классов и композиции родов квадратичных форм.

Не вдаваясь в эту сложную теорию Гаусса, мы приведем его результаты о числе родов и о числе классов в каждом роде.

Каждый род собственно примитивного порядка содержит одно и то же число классов,

Рекомендуем скачать другие рефераты по теме: ответы по математике, как написать дипломную работу.





Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата