Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10 | Следующая страница реферата

f/(x) = –sin x+x>0 (или sin x< x). Т.е., функция f(x) для x³0 возрастающая, а при x<0 будет f(x)>f(0)=0, т.е. cos x>1–(1/2)x2.

Отсюда, аналогично при x>0 получим sin x>x–(1/6)x3.

Задача 1.10. Доказать, что при 0<x<p/2 выполняется tg x > x+(1/3)x3.

Для этого достаточно установить, что для указанных x производная функции tg x–x–(1/3)x3, равна sec2x–1–x2, положительна, т.е. что tg2x – x2>0, а это приводит к известному неравенству tg x>x.

Задача 1.11. Доказать, что при x>0 выполняется ln x £ x-1.

Так как функция f(x)=ln x–x (x>0) имеет производную f/(x)=(1/x)–1 > 0 (при 0<x<1) и f/(x)=(1/x)–1 < 0 (при x>1), то функция возрастает пока x изменяется на промежутке (0,1], и убывает на промежутке [1;+¥). Отсюда получаем, что f(1)=–1 будет наибольшим значением функции, так что для x>0 выполняется ln x £ x-1.

1.3. Применение производной при решении уравнений

Покажем, как с помощью производной можно решать вопросы существова-ния корней уравнения, а в некоторых случаях и их отыскания. По-прежнему основную роль здесь будут играть исследования функции на монотонность, нахождение ее экстремальных значений. Кроме того, будет использован ряд свойств монотонных и непрерывных функций.

Свойство 1. Если функция f возрастает или убывает на некотором промежутке, то на этом промежутке равнение f(x)=0 имеет не более одного корня.

Это утверждение вытекает непосредственно из определения возрастающей и убывающей функций. Корень уравнения f(x)=0 равен абсциссе точки пересечения графика функции y=f(x) с осью x.

Свойство 2. Если функция f определена и непрерывна на промежутке [a,b] и на его концах принимает значения разных знаков, то между a и b найдется точка c, в которой f(c )=0.

Задача 1.12. Решить уравнение  

Решение.

Заметим, что  является корнем уравнения. Докажем, что других корней это уравнение не имеет. Исследуем функцию f, где , на монотонность. Производная . Установим промежутки, на которых функция  сохраняет знак. Для этого исследуем ее на монотонность. Производная . Так как при  , то  при . Следовательно, функция  возрастает при положительных значениях x; . Поэтому  при . В силу четности функции  она принимает положительные значения при всех . Следовательно, f возрастает на всей числовой оси. Согласно свойству 1, уравнение  имеет не более одного корня. Итак,  – единственный корень уравнения.

Задача 1.13. Решить систему уравнений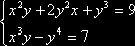  

Решение.

Система эквивалентна следующей: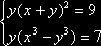

Из первого уравнения следует, что , из второго – . Выразим з первого уравнения x через y: , . Тогда 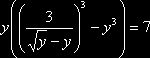. положив , получим 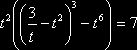 или . Производная функции f, где , равна . она отрицательна при всех значениях t. Таким образом, функция f убывает. Поэтому уравнение  имеет не более одного корня. Заметим, что  является его корнем. Итак,  единственное решение системы.

Задача 1.14. Доказать, что уравнение  имеет единственный корень, лежащий в интервале .

Решение.

Уравнение равносильными преобразованиями приводится к виду , где . Функция f возрастающая, так как  при всех . Согласно свойству 1, уравнение имеет не более одного решения. Функция f непрерывна, кроме того, , . В силу свойства 2 уравнение на интервале  имеет корень.

В задаче 3 требовалось доказать, что корень уравнения принадлежит некоторому промежутку. Мы пользовались свойством 2 непрерывной на отрезке функции, принимающей на концах этого отрезка значения разных знаков. Этот путь не всегда приводит к цели при решении подобных задач. Иногда целесооб-разно воспользоваться следующим свойством дифференцируемых функций.

Свойство 3 (Теорема Ролля). Если функция f непрерывна на отрезке [a,b], дифференцируема на интервале (a,b) и f(a)=f(b), то существует точка  такая, что .

 На геометрическом языке свойство 3 означает следующее: если , то на графике кривой  найдется точка С с координатами , где касательная к графику параллельна оси x.

Задача 1.15. Доказать, что уравнение  при ,  имеет не более одного действительного корня.

Решение.

Рекомендуем скачать другие рефераты по теме: диплом управление, бесплатные тесты.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10 | Следующая страница реферата