Предыдущая страница реферата | 9  10  11  12  13  14  15  16  17  18  19 | Следующая страница реферата



и потому 5х2 - 44х + 68 = 0. Значит, для нахождения х надо решить уравнение

5х2 - 44х + 68 = 0.

Решая его, находим D = (- 44)2 - 4× 5× 68 = 1936 - 1360 = 576,

Х1,2 = (44 ± 24) / 10.

Итак х1 = 6,8; х2 = 2, Þ у1 = 11 - 2× 6,8 = - 2,6; у2 = 11 - 2× 2 = 7.

Ответ: х1 = 6,8; у1 = - 2,6; х2 = 2; у2 = 7.

Метод введения новых неизвестных при решении уравнений и систем уравнений.

При решении биквадратных и возвратных уравнений мы вводили новые неизвестные (у = х2 для биквадратных уравнений и у = х + 1 / х для возвратных уравнений). Введение новых неизвестных применяется также при решении уравнений иного вида и систем уравнений.

Пример 7.28. Решим уравнение 12 / (х2 + 2х) - 3 / (х2 + 2х - 2) = 1.

Решение. Если попробовать привести дробь в левой части уравнения к одному знаменателю, то получим уравнение четвёртой степени, которое мы умеем решать. Чтобы решить заданное уравнение, заметим, что в обе дроби входит одно и то же выражение х2 + 2х. Поэтому введём новое неизвестное у, положив, что у = х2 + 2х. Тогда уравнение примет вид

12 / у - 3 / (у - 2) = 1 или (у2 - 11у + 24) / (у(у - 2)) = 0,

откуда y1 = 3; y2 = 8. Осталось решить уравнения х2 + 2х = 3 (его корни х1 = 1, х2 = - 3) и х2 + 2х = 8 (его корни х3 = 2, х4 = - 4).

Применённый метод называется методом введения новых неизвестных, и его полезно применять, когда неизвестное входит в уравнение всюду в виде одной и той же комбинации (особенно если эта комбинация содержит степени неизвестного выше первой).

Пример 7.29. Решим систему уравнений

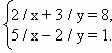
Решение. Обозначим 1 / х через U, а 1 / у через V. Тогда система примет вид

т.е. получится система двух линейных уравнений с двумя неизвестными U и V. Из первого уравнения выражаем U через V: U = 4 - 3V / 2, и подставляя во второе: 5(4 - 3V / 2) - 2V = 1, откуда V = 2. Теперь находим U = 1 и решаем уравнения 1 / x = 1, 1 / y = 2.

Ответ: x = 1, y = 0,5.

Пример 7.30.

(x – 4)(x – 5)(x – 6)(x – 7) = 1680.

Решение. (x – 4)(x – 7)× (x – 5)(x – 6) = 1680, т.е.

(x2 – 11x + 28)(x2 – 11x + 30) = 1680.

Обозначим x2 – 11x + 28 = t, тогда t(t + 2) = 1680, t2 + 2t – 1680 = 0, t1 = – 42; t2 = 40. Поэтому

x2 – 11x + 28 = – 42; x2 – 11x + 70 = 0; D = 121 – 280 < 0 Þ x1,2 Î Æ .

x2 – 11x + 28 = 40; x2 – 11x – 12 = 0; x1 = 12; x2 = – 1.

Рекомендуем скачать другие рефераты по теме: первый снег сочинение, научный журнал.

Предыдущая страница реферата | 9  10  11  12  13  14  15  16  17  18  19 | Следующая страница реферата