Различные подходы к определению проективной плоскости
| Категория реферата: Рефераты по математике
| Теги реферата: цивилизация реферат, человек реферат
| Добавил(а) на сайт: Karantirov.
Предыдущая страница реферата | 11 12 13 14 15 16 17 18 19 20 21 | Следующая страница реферата
Разделив произведение первых трех соотношений на произведение последних двух, производя сокращение, мы получаем:
(VP/WP)*(WQ/UQ)*(UR/VR)=1
то есть P,Q,R коллинеарны, теорема доказана.
Приложение№1. Если два треугольника перспективны относительно точки и две пары соответствующих сторон параллельны, то и две оставшиеся стороны параллельны.
Дано: треугольник PRQ и треугольник P’R’Q’ перспективны относительно точки О. QR||Q’R’, PR||P’R’
Доказать что: QP||Q’P’
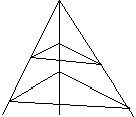
Доказательство:
Так как QR||Q’R’ и RP||R’P’, то
(OQ/OQ’)=(OR/OR’)=(OP/OP’) Þ (OQ/OQ’)=(OP/OP’) Þ QP||Q’P’
№2.Назовите два треугольника перспективных относительно:
а) точки Р
б) точки Р’
в) точки D
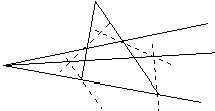
Ответы: а) треугольники ROQ и EP’F б) треугольники EFP и R’Q’O’ в) треугольники R’RE и Q’QF.
№3. Если А,С,Е - три точки на одной прямой, B,D,F- на другой, и если прямые АВ и CD параллельны прямым DE и FA соответственно, то прямые EF||BC.
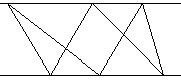АС||BD. Рассмотрим параллелограмм ABDE и AFDC Þ
BD=AE и DF=AC. Произведем вычитание BD-DF=BF; AE-AC=CE Þ
BF=CE Þ BCEF - параллелограмм Þ
EF||BC. 
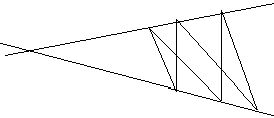ACÇ BD=0, так как AB||ED и CD||FA, то
(|OA|/|OB|)=(|OE|/|OD|) и (|OC|/|OD|)=(|OA|/|OF|) получаем |OB|*|OE|=|OA|*|OD|=|OC|*|OF|
Þ
(|OE|/|OF|)=(|OC|/|OB|) Þ EF||CB.
№4. Пусть A,B,D,E,N,M - шесть точек, обладающих тем свойством, что прямые AE,DM,NB пересекаются в одной точке и прямые АМ,DB,NE пересекаются в одной точке. Что можно сказать о прямых AB,DE,NM?
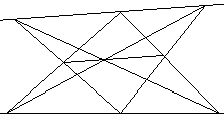
Решение. Пусть AEÇ DMÇ NB=C, AMÇ DBÇ NE=F обозначим () пересечения прямых АВ и DE через L. По теореме Паппа ()LÎ MN Þ ABÇ DEÇ MN=L. Прямые AB,DE,NM пересекаются в одной точке.
№5. Доказать, что медианы треугольника пересекаются в одной точке.
AA’Ç BB’Ç CC’=S ?
Решение: Рассмотрим треугольник АВС и треугольник А1В1С1- дезарговые треугольники, то есть треугольники удовлетворяют теореме Дезарга.
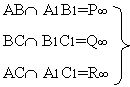
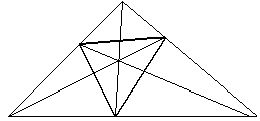
лежат на одной несобственной прямой S¥
по обратной теореме Дезарга прямые, проходящие через соответствующие вершины, пересекаются в одной точке S.
AA’Ç BB’Ç CC’=S.
Рекомендуем скачать другие рефераты по теме: конспект урока 8 класс, шпаргалка егэ.
Категории:
Предыдущая страница реферата | 11 12 13 14 15 16 17 18 19 20 21 | Следующая страница реферата
Главная