Предыдущая страница реферата | 11  12  13  14  15  16  17  18  19  20  21 | Следующая страница реферата



№11. Сформулировать в терминах евклидовой геометрии теорему Дезарга для случая:

()S¥ - несобственная (), дезаргова прямая S - собственная.

Формулировка теоремы Дезарга: Если прямые проходящие через соответствующие вершины двух треугольников параллельны, то точки пересечения соответствующих сторон лежат на одной прямой.

()S собственная, прямая S¥ - несобственная.

Формулировка.

Если прямые, походящие через соответствующие вершины двух треугольников АВС и А’В’С’ пересекаются в одной точке и AB||A’B’, B’C||BC, то AC||A’C’.

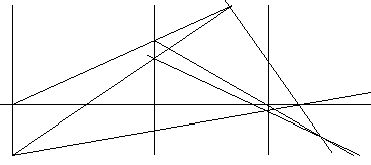
3) ()S¥ - несобственная, прямая S¥ - несобственная.

Формулировка.

Если прямые проходящие через соответствующие вершины двух треугольников параллельны и AB||A’B’, BC||B’C’, то AC||A’C’.

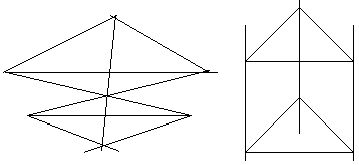
№12. Прямая p лежит в плоскости треугольника АВС; К=ВСÇ p, L=ACÇ p, M=ABÇ p, R=BLÇ CM, S=CMÇ AK, T=AKÇ BL.

Доказать, что прямые AR,BS и CT пересекаются в одной точке.

Требуется доказать, что ARÇ BSÇ CT=Q

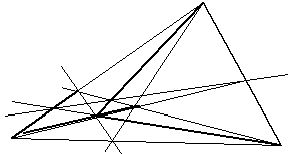
Решение

Треугольники АВС и RST - дезарговы треугольники.

M,K,LÎ з (по условию)

Таким образом, по теореме обратной теореме Дезарга ARÇ BSÇ CT=Q.

№13. Даны прямые a и b, пересекающиеся в точке S, которая лежит за пределами чертежа. Дана ()С не лежащая ни на одной из данных прямых. Построить прямую SC.

Построение.

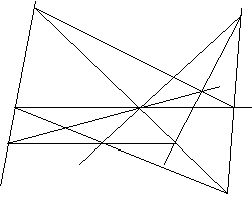
Выбираем произвольно прямую s, () A,A’Î a и ()ВÎ b.

1)ABÇ s=P,2)PA’Ç b=B’,3)ACÇ s=R,

4)BCÇ s=Q,5)A’R, B’Q,6)B’QÇ A’R=C’,

7)CC’ искомая прямая.

Доказательство:

Треугольники АВС и А’В’С’ - дезарговы треугольники, прямая s - дезаргова прямая.

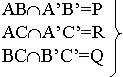Î s (по построению)

По обратной теореме Дезарга AA’Ç CC’Ç BB’=S.

Рекомендуем скачать другие рефераты по теме: конспект урока 8 класс, шпаргалка егэ.





Предыдущая страница реферата | 11  12  13  14  15  16  17  18  19  20  21 | Следующая страница реферата