Пределы последовательностей и функций

| Категория реферата: Рефераты по математике
| Теги реферата: воспитание реферат, атанасян решебник
| Добавил(а) на сайт: Vorozhcov.

Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 | Следующая страница реферата

. (4.1)

Предел (4.1) может не существовать. В этом случае говорят, что функция не имеет производной в точке . Если предел (4.1) равен , то говорят, что функция имеет в точке бесконечную производную.

В различных задачах (в том числе и экономических) производная функции интерпретируется как скорость изменения величины y относительно x. Геометрический смысл производной состоит в том, что – это тангенс угла наклона касательной к графику в точке .

Нахождение производной функции называется дифференцированием этой функции. Если функция в точке х имеет конечную производную, то функция называется дифференцируемой в этой точке.

Укажем правила дифференцирования, которые сводят вычисление производных одних функций к вычислению производных других (более простых) функций.

Если функции дифференцируемы в точке , то сумма, разность, произведение и частное этих функций также дифференцируемы в точке , и справедливы следующие формулы

Если функция имеет обратную функцию и в точке производная , то обратная функция дифференцируема в точке и или .

Если функция дифференцируема в точке и , то сложная функция также дифференцируема в и верна следующая формула

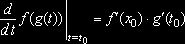или .

Пример.

Найти производную функции

Решение:

3 Геометрические изложения и дифференцированные исчисления (построение графиков)

Функция , определенная во всех точках промежутка , называется возрастающей (убывающей) в этом промежутке, если для любых двух значений аргумента, принадлежащих этому промежутку, большему из них соответствует большее (меньшее) значение функции, т. е,

если то при

– возрастающая, – убывающая.

Из данного определения вытекает, что для возрастающей функции приращения аргумента и функции имеет один и тот же знак, в силу чего их отношение положительно: . Для убывающей функции эти приращения имеют разные знаки, в силу чего . Те значения аргумента, при которых функция достигает своих наибольших и наименьших по сравнению с близкими значений, называются точками максимума и минимума (точками экстремума).

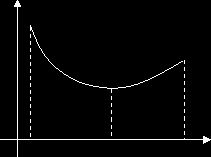
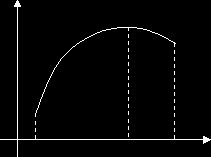
Точка называется точкой максимума (минимума) непрерывной функции , а значение называется максимумом (минимумом) этой функции, если существует некоторая окрестность точки такая, что значение функции в любой точке этой окрестности будет меньше (больше), чем ее значение в самой точке , т. е. меньше (больше), чем максимум (минимум) (рис. 1).

у max у

min

f(х0) f(х0)

О х0–d х0 х0+d х О х0–d х0 х0+d х

точка максимума

Рекомендуем скачать другие рефераты по теме: дипломная работа аудит, предмет культурологии.

Claw.ru | Рефераты по математике | Пределы последовательностей и функций

Пределы последовательностей и функций

Категории:

Поделитесь этой записью или добавьте в закладки

Рефераты от А до Я

Полезные заметки