Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата

Функция претерпевает разрыв в точке .

Найдем асимптоты графиков функции:

а). Прямая  является вертикальной асимптотой, т.к.

,      

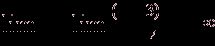б). Находим наклонные и горизонтальные асимптоты (горизонтальные асимптоты являются частным случаем наклонных асимптот) ,

где                     ;

Таким образом, прямая  является единственной наклонной асимптотой и на , и на .

Найдем точки пересечения графика функции с осями координат.

а) С осью : , , т.е. точка пересечения с осью  - .

б) С осью : , , т.е. точка пересечения с осью  - .

6. Исследуем функцию на возрастание, убывание и экстремум. Для этого найдем производную функции.

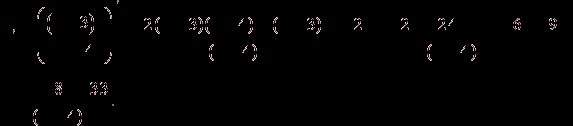
Из  получаем , откуда , .

+                                   _                                +

______________________________________  x

-3                                              11

Так как на интервалах  и  производная положительна, т.е. , то график функции на указанных интервалах возрастает. Так как на интервале  производная отрицательна, т.е. , то на указанном интервале график функции убывает.

Так как при переходе через точки ,  производная функции меняет знаки и эти точки входят в область определения функции, то ,  - точки локального экстремума. Причем  точка локального минимума:  (так как при переходе через нее производная меняет знак с "+" на "-");  - точка локального максимума:  (так как при переходе через нее производная меняет знак с "-" на "+").

7. Исследуем график функции на выпуклость, вогнутость и определим точки перегиба. Для этого найдем вторую производную функции.

Очевидно, что в интервале  вторая производная меньше нуля, т.е. , и в этом интервале график функции является выпуклым вверх. В интервале  вторая производная больше нуля, т.е. , и в этом интервале график функции является выпуклым вниз (вогнутым).

Несмотря на то, что при переходе через точку  вторая производная меняет знак, она не является точкой перегиба, так как  не входит в область определения функции, т.е. функция в ней не определена. Таким образом, точек перегиба у графика функции нет.

Из  получаем , откуда , .

+                                   _                                +

Рекомендуем скачать другие рефераты по теме: дипломная работа аудит, предмет культурологии.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата