Предыдущая страница реферата | 3  4  5  6  7  8  9  10  11  12  13 | Следующая страница реферата

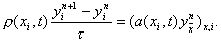(25)

Предположим, что коэффициенты r (xi, t), a(xi, t) – постоянные, r (xi, t) є = const, a(xi, t) є a = const. Тогда уравнение (25) можно записать в виде

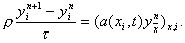
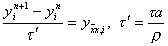или

Из п.2 известно, что последнее уравнение устойчиво при t 0,5h2, т.е. при

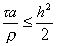(26)

Принцип замороженных коэффициентов утверждает, что схема (25) устойчива, если условие (26) выполнено при всех допустимых значениях a(xi, t), r (xi, t), т.е. если при всех x, t выполнены неравенства

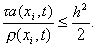(27)

Если известно, что 0 < c1 Ј a(xi, t) Ј c2, r (xi, t) і c3 > 0, то неравенство (27) будет выполнено при

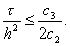
Строгое обоснование устойчивости схемы (25) будет дано в примере 2 из главы 2.

Если параметр s 0,5, то из принципа замороженных коэффициентов следует абсолютная устойчивость схемы (24).

Рассмотрим теперь первую краевую задачу для нелинейного уравнения теплопроводности

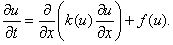(28)

В случае нелинейных уравнений, когда заранее неизвестны пределы изменения функции k(u), избегают пользоваться явными схемами. Чисто неявная схема, линейная относительно yin+2, i = 1, 2,…, N – 1, имеет вид

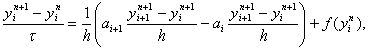(29)

где ai = 0,5 (k(yni) + k(yni-1)). Эта схема абсолютно устойчива, имеет первый порядок аппроксимации по t и второй – по h. Решение yin+1, i = 1, 2,…, N – 1, находится методом прогонки. Заметим, что схему (29) можно записать в виде

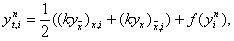
где ki = k(yin).

Часто используется нелинейная схема

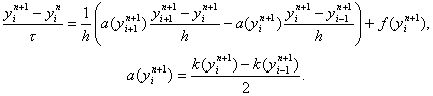(30)

Для реализации этой схемы необходимо применить тот или иной итерационный метод. Например такой:

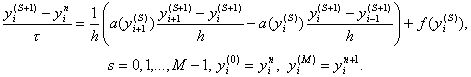(31)

Здесь s – номер итерации. Как видим, нелинейные коэффициенты берутся с предыдущей итерации, а в качестве начального приближения для yin+1 выбирается yin. Это начальное приближение тем лучше, чем меньше шаг t . Число итераций M задается из соображений точности. В задачах с гладкими коэффициентами при k(u) і c1 > 0 часто бывает достаточно провести две – три итерации. Значения yi(S+1) на новой итерации находятся из системы (31) методом прогонки. При M = 1 итерационный метод (31) совпадает с разностной схемой (29).

Для приближенного решения нелинейного уравнения (28) применяются также схемы предиктор – корректор второго порядка точности, аналогичные методу Рунге – Кутта для обыкновенных дифференциальных уравнений. Здесь переход со слоя n на слой n+1 осуществляется в два этапа. Приведем пример такой схемы. На первом этапе решается неявная линейная система уравнений

Рекомендуем скачать другие рефераты по теме: понятие культуры, баллов.





Предыдущая страница реферата | 3  4  5  6  7  8  9  10  11  12  13 | Следующая страница реферата