Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

Это утверждение сразу следует из явного представления коэффициентов (5), (6).

Воспользовавшись (19), оценим слагаемые, входящие в левую часть тождества (18), следующим образом:

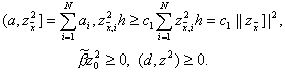
Тогда придем к неравенству

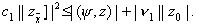(20)

Оценим сверху правую часть этого неравенства. Будем иметь

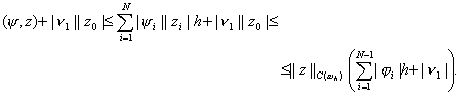
Подставляя эту оценку в (20) и учитывая неравенство (17), получим

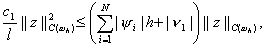
т.е.

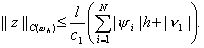
Окончательно

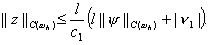(21)

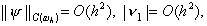
Посколькуиз неравенства следует,

что погрешность zi = yi – u(xi) также является величиной O(h2) при h® 0. Итак, справедливо следующее утверждение.

Пусть k(x) – непрерывно дифференцируемая и q(x), f(x) – непрерывные функции при xО [0, l], решение u(x) задачи (1), (2) обладает непрерывными четвертыми производными. Пусть коэффициенты разностной схемы (3), (4) удовлетворяют условиям (8), (9), (19). Тогда решение разностной задачи (3), (4) сходится при h® 0 к решению исходной дифференциальной задачи (1), (2) со вторым порядком по h, так что выполняется оценка

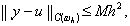
где M – постоянная, не зависящая от h.

3. Разностные схемы для уравнения теплопроводности 3.1. Исходная задача.

Будем рассматривать следующую первую краевую задачу для уравнения теплопроводности с постоянными коэффициентами. В области {0 < x < 1, 0 < t Ј T} требуется найти решение уравнения

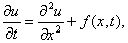(1)

удовлетворяющее начальному условию

u(x, 0) = u0(x)(2)

и граничным условиям

u(0, t) = m 1(t), u(1, t) = m 2(t).(3)

Рекомендуем скачать другие рефераты по теме: понятие культуры, баллов.





Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата