Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

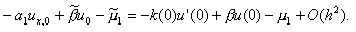
Докажем последнее утверждение. Используя разложение

ux, 0 = (u1 – u0)/h = u’(x1/2) + O(h2), x1/2 = 0,5h,

a1 = k1/2 + O(h2)

получим

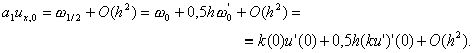
Отсюда имеем

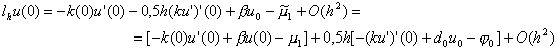
Учитывая граничное условие (2), получаем

lhu(0) = 0,5h [– (ku’)’(0) + d0u0 – j 0] + O(h2).

Выражение, стоящее в квадратных скобках, преобразуем, учитывая уравнение (1), к виду

– (ku’)’(0) + d0u0 – j 0 = – (ku’)’(0) + q(0)u(0) – f(0) +

+ (d0 – q(0))u0 – (f(0) – j 0) = (d0 – q(0))u0 – (f(0) – j 0).

Из соотношений

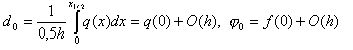
получаем

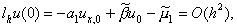
что и требовалось доказать.

Таким образом, при достаточной гладкости коэффициентов k(x), q(x), f(x) и решения u(x) разностная схема (10) аппроксимирует исходную задачу (2) со вторым порядком по h.

При практическом использовании разностной схемы для нахождения ее коэффициентов не обязательно вычислять интегралы (4), (6) точно. Можно воспользоваться коэффициентами, полученными путем замены этих интегралов квадратурными формулами, имеющими точность O(h2) и выше. Например, в результате применения формулы прямоугольников получим следующие коэффициенты: ai = k(xi – 0,5h), di = q(xi), j i = f(xi).

Применяя формулу трапеций, получим

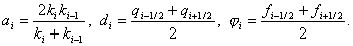
Представление коэффициентов разностной схемы в виде интегралов (4), (6) оказывается полезным при исследовании сходимости в случае разрывных функций k(x), q(x), f(x).

2.3. Уравнение для погрешности.

Решение yi = y(xi) разностной задачи (3), (4) зависит от шага h сетки, y(xi) = yh(xi). По существу, мы имеем семейство решений {yh(xi)}, зависящее от параметра h. Говорят, что решение yh(x) разностной задачи сходится к решению u(x) исходной дифференциальной задачи, если при h® 0 погрешность yh(xi) – u(xi), i = 0, 1,…, N, стремится к нулю в некоторой норме. В настоящем параграфе в качестве такой нормы будем брать норму в сеточном пространстве C(w h), т.е. положим

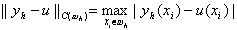
Рекомендуем скачать другие рефераты по теме: понятие культуры, баллов.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата