
Разностные аппроксимации
| Категория реферата: Рефераты по математике
| Теги реферата: бесплатные рефераты без регистрации, судебная реферат
| Добавил(а) на сайт: Шипулин.
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 11 | Следующая страница реферата
Говорят, что разностная схема имеет m-й порядок точности (или сходится с порядком m), если
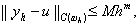
где m>0, M>0 – константы, не зависящие от h.
Выше было установлено, что схема (3), (4) имеет второй порядок аппроксимации. Докажем теперь, что эта схема имеет и второй порядок точности. Для этого прежде всего выпишем уравнение, которому удовлетворяет погрешность zi = yi – u(xi). Поставим yi = zi + u(xi) в уравнения (3), (4). Тогда получим уравнения
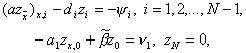 (11), (12)
(11), (12)
где обозначено
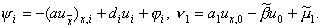
Функция y i, входящая в правую часть уравнения (11), называется погрешностью аппроксимации дифференциального уравнения (1) разностным уравнением (3) на решении задачи (1), (2). В п.1 было доказано, что y i = O(h2) при h® 0, i=1, 2,…, N–1. Аналогично, величина n 1 является по определению погрешностью аппроксимации краевого условия (2) разностным краевым условием (4) на решении задачи (1), (2), причем n 1=O(h2). Таким образом, структура уравнений для погрешности (11), (12) та же, что и у разностной схемы (3), (4), отличаются только правые части.
Чтобы доказать сходимость разностной схемы, оценим решение задачи (11), (12) через правые части y i, n 1, т.е. получим неравенство вида
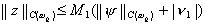 (13)
(13)
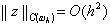 с константой M1, не зависящей от h. Из этого неравенства и будет следовать, что
с константой M1, не зависящей от h. Из этого неравенства и будет следовать, что
Отметим, что неравенства вида (13), называемые априорными оценками, нашли широкое применение в теории разностных схем. Поскольку структура для погрешности (11), (12) та же, что и у разностной схемы (3), (4), а отличаются только правые части, то оценка (13) выполняется одновременно с аналогичной оценкой
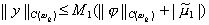
для разностной схемы (3), (4) при m 2 = 0. Последняя оценка выражает устойчивость решения разностной задачи по правым частям j и m 1.
2.4. Разностные тождества и неравенства.Для того, чтобы доказать неравенство (13), нам потребуются некоторые разностные тождества и неравенства. Будем рассматривать сеточные функции, заданные на сетке (7). Обозначим
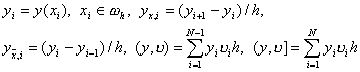
Справедливо следующее разностное утверждение:
(y, u x) = –(u , yx) + yNu N – y0u 1.(14)
Действительно,
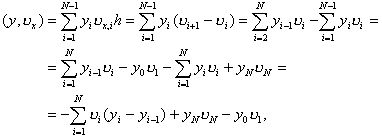
что и требовалось доказать. Тождество (14) называется формулой суммирования по частям.
Подставляя в (14) вместо u выражение azx и вместо y функцию z, получаем первую разностную формулу Грина
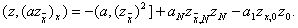 (15)
(15)
Здесь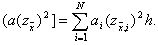
В частности, если zN = 0 (как в задаче (11), (12)), то получим
Рекомендуем скачать другие рефераты по теме: понятие культуры, баллов.
Категории:
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 11 | Следующая страница реферата
 Главная
Главная