Замечание: Определение всех классов колец предоставляется сформулировать читателю.
|
Опр.3 |
Коммутативное кольцо с единицей без делителей нуля называеться областью |
целостности.
Примером области челосности является кольцо Z , колцо многочленов от одной переменной K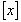 , где К- область челостности.
, где К- область челостности.
Так как кольцо это алгебра, а алгебра это множество, то есть смысл говорить о его
подмножествах, среди которых особый интерес представляют подкольца.
|
Опр.4 |
Подмножество I кольца К называется его подкольцом, если оно само является |
кольцом относительно операции кольца К .
Для проверки является ли рассматриваемое подмножество кольца К его подкольцом удобно пользоваться критерием подкольца.
|
Теорема 5. |
(критерий подкольца) Подмножество I кольца К является подкольцом |
тогда и только тогда, когда оно замкнуто относительно вычитания элементов и умножения , т.е. если (1) 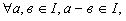
(2) 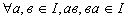
Ü
Пусть
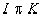
(где “
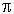
,,- “ быть подкольцом ,,) .Покажем что (1) и (2) имеют место.
Так как 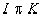 , то он является кольцом, а кольцо это абелева група, тогда для
, то он является кольцом, а кольцо это абелева група, тогда для 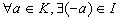 , поэтому
, поэтому 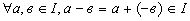 следовательно (1) выполнено. Выполнимость (2) вытекает из того что I замкнуто относительно умножения.
следовательно (1) выполнено. Выполнимость (2) вытекает из того что I замкнуто относительно умножения.
Пусть
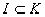
, (1),(2) – выполнены. Покажем, что I – подкольцо, т.е. что I – кольцо.
Для этого проверим выполнимость всех аксиом кольца. Из (2) следует, что I – замкнуто относительно умножения, ассоциативность умножения следует из того,что 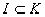 .
.
Рассмотрим условие (1). Пусть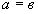
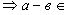
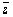 ,но
,но 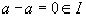 ,
, 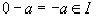 , ассоциатив -ность сложения вытекает из того что
, ассоциатив -ность сложения вытекает из того что 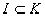 . Таким образом, все аксиомы кольца имеют место в I, следовательно, I – кольцо. Так как
. Таким образом, все аксиомы кольца имеют место в I, следовательно, I – кольцо. Так как 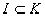 , то это подкольцо.
, то это подкольцо.
Интересен случай подкольца, когда оно является идеалом. Введём это понятие.
|
Опр. 6 |
Подкольцо I кольца K называется идеалом если для 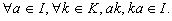 |
В кольце с 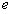 существует особый идеал:
существует особый идеал: 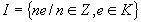 Такой идеал называется главным идеалом. Главный идеал является наименьшим подкольцом, образованным
Такой идеал называется главным идеалом. Главный идеал является наименьшим подкольцом, образованным 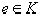
Пусть К является областью целостности. Зададим на нём отношение “сравнения по идеалу I ”.
|
Опр.7 |
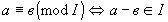 . Легко проверить, что “ . Легко проверить, что “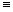 “ – отношение эквивалентности: “ – отношение эквивалентности: |
Рекомендуем скачать другие рефераты по теме: бесплатные конспекты, реферат на тему види.
Предыдущая страница реферата |
7
8
9
10
11
12
13
14
15
16
17 |
Следующая страница реферата

![]()
 Главная
Главная