Предыдущая страница реферата | 17  18  19  20  21  22  23  24  25  26  27 | Следующая страница реферата

Определение 1. Поле P называется алгебраически замкнутым, если любой многочлен положительной степени имеет в этом поле корень. Алгебраической замкнутостью обладает поле C, это решается основной теоремой алгебры.

Теорема 2. Любой многочлен положительной степени из кольца C[x] обладает по крайней мере одним корнем. Примем эту теорему без доказательства в силу того, что она требует предварительного доказательства ряда теорем из математического анализа.

Из основной теоремы алгебры вытекает ряд следствий, их и рассмотрим.

Следствие 3. Неприводимым над полем C многочленом является многочлен только первой степени.

Для доказательства этого утверждения введем определения приводимого и неприводимого многочлена. Многочлен f(x)Î P[x] называется приводимым, если его можно представить в виде произведения двух многочленов меньшей положительной степени. В противном случае многочлен называется неприводимым.

Приступим к доказательству следствия 3.

Пусть дан f(x)Î C[x]. Пусть он приводим. Покажем, что

рассмотрим f(x)=a1x+a0, degf(x)=1. Предположим, что f(x) – приводим. Тогда по определению приводимого многочлена f(x)=f1(x)f2(x), где degf1(x)>0, degf2(x)>0. Однако по условию degf(x)=1=1+0=0+1, то есть degf1(x)=0È degf2(x)=0, что противоречит свойству степеней. Полученное противоречие и доказывает неприводимость многочлена (а1х+а0).

Пусть deg f(x)>1, тогда по основной теореме алгебры он обладает корнем. Пусть таким корнем будет х=а. По следствию из теоремы Безу: f(x)=(x-a)f1(x). Так как deg(x-a)=1, degf(x)>1, deg(x-a)f1(x)=deg(x-a)+degf1(x), то degf(x)>0; то есть f(x) – приводим, что противоречит условию. Таким образом, неприводимым над полем С является только многочлен первой степени.

Следствие 4. Если f(x)Î C[x], degf(x)=n³ 1, то его можно представить в виде:

с(x-a1)(x-a2)...(x-an), (*)

где ai – корни его, а сÎ С.

g Пусть f(x)=c1x+c0=c1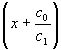=c1(x-a1), где ,то есть для многочлена f(x) утверждение верно: он представляется в виде (*) и а1– корень его, а с1– старший коэффициент.

Далее, проведем доказательство методом математической индукции. Пусть теорема верна для многочлена степени меньшей или равной (n-1), то есть

f(x)=c(x-a1)...(x-an-1), где a1, a2, ..., an-1– его корни, а с – старший коэффициент.

Пусть f(x) – неприводим, а это возможно только для n=1, для этого случая теорема верна. Либо f(x) – приводим, тогда f(x)=g(x)h(x), где степени g(x) и h(x) меньше n, для них теорема верна. В силу свойства степени f(x)=c(x-a1)...(x-an), то есть множителей будет ровно n. По следствию из теоремы Безу аi – корни f(x), если расткрыть скобки в правой части и воспользоваться равенством многочленов, то с – старший коэффициент f(x). Теорема доказана.

Из этого в следствии с необходимостью вытекает еще два.

Следствие 5. Количество комплексных коней многочлена f(x)Î C[x] совпадает с его степенью.

Следствие 6. Любой многочлен f(x)Î C[x] положительной степени n можно представить в виде:

f(x)=c(x-a1)a 1(x-a2)a 2...(x-ak)a k, где a 1+...+a k=n, ai – его корни. Такое представление носит название канонического. Возможность такого представления вытекает из следствия (4) и допустимости повторяющихся корней, то есть кратных корней многочлена.

В теории многочленов над С имеет место теорема, устанавливающая связь между корнями многочлена и его коэффициентами.

Теорема 7. Пусть f(x)Î C[x], degf(x)=n, an=1 (то есть f(x) – нормирован), тогда как известно, f(x)=(x-a1)(x-a2)...(x-an), где имеет место соотношение:

а0 = (-1)n a1 a2 ... an;

a1= (-1)n-1 (a1a2 ... an-1+ ... + a2a3 ... an);

. . . . . . . . .

an-2= a1a2+ a1a3+ ... + an-1an ;

an-1= -(a1+ a2+ ... +an);

эти соотношения называются формулами Виета. Однако, справедливости ради, надо отметить, что Виет нашел эту зависимость только для случая положительных корней, в общем виде эта теорема установлена А. Жирарое.

Вопрос 12 Кольцо многочленов над полем действительных чисел (R).

В алгебре имеет место теория многочленов. Многочлен введен по определению как выражение f(x)=anxn+an-1xn-1+...+a1x+a0, где aiÎ K – кольцо, x0=1, 1·x= x. Введение операций “+” и “´ ” многочленов позволило построить алгебру многочленов, которой является кольцо многочленов над кольцом К и обозначается К[x]. Особый интерес представляет теория многочленов, когда вместо кольца К взято поле. Такими числовыми полями являются C, R, Q.

В силу существования операции деления в поле, стало возможным рассматривать два взаимосвязанных вопроса в теории многочленов: корни многочлена и разложение многочлена на неприводимые многочлены.

Рассмотрим решение этой проблемы для кольца многочленов над R.

Теорема 1. Комплексные корни f(x)Î К[x], то есть с действительными коэффициентами попарно сопряженными.

n Пусть f(x)Î К[x], и пусть z=a+bi; a,bÎ R комплексное число, являющееся корнем f(x), причем degf(x)³ 2 в противном случае f(x) комплексных корней иметь не может. Покажем, что =a–bi, b¹ 0 тоже является корнем f(x).

f()=ann+an-1n-1+...+a1+a0= (воспользуемся свойством сопряжения) = =, то есть является корнем f(x), что и требовалось доказать.

Рассмотренная выше теорема позволяет доказать теорему о неприводимом многочлене из R[x]. Напомним определение приводимого и неприводимого многочленов.

f(x) называется неприводимым, если его можно представить в виде произведения двух многочленов меньшей положительной степени и неприводимым, если этого сделать нельзя.

Рассмотрим f(x)= a1x+a0, aiÎ R. его нельзя представить в виде произведения двух многочленов меньшей положительной степени в силу того, что 1=1+0=0+1.

Решать будем вопрос о приводимости и неприводимости многочлена f(x)Î R[x] степени большей или равной 2.

Теорема 2. Неприводимый многочлен f(x)Î R[x], degf(x)=n³ 2 ассоциирован с многочленами (x-a)2+b2,где x=a+bi комплексный его корень.

n Пусть f(x)Î R[x], degf(x)=n³ 2, пусть x=a+bi, b¹ 0 – корень f(x), он неприводим.

Прежде всего отметим, что у такого многочлена нет действительных корней, иначе бы f(x)=(x-a) f1(x) (следствие из теоремы Безу), что противоречило бы его неприводимости.

По теореме о сопряженности мнимых корней многочлена с действительными коэффициентами f(x) обладает еще одним корнем x2=a–bi, где x2=.

Рассмотрим (x-x1)(x-x2)=(x-a)2+b2. (*)

Разделим f(x) на многочлен (*), получим:

f(x)=[(x-a)2+b2]g(x)+r(x).

Так как степень делителя равна 2, то degr(x)<2, то есть r(x)=cx+d. Подставим в (1) x1=a=bi и x2=a-bi, мы получим:

Так как b¹ 0 , то c=0, тогда d=0, то есть r(x)=.

Это означает, что f(x)M (*). Но f(x) – неприводим, потом deg g(x)=0, то есть g(x)Î R. Что и подтверждает ассоциированность f(x) и (*).

Теорема 3. Рассмотренная выше теорема позволит сделать ряд выводов:

Рекомендуем скачать другие рефераты по теме: бесплатные конспекты, реферат на тему види.





Предыдущая страница реферата | 17  18  19  20  21  22  23  24  25  26  27 | Следующая страница реферата